Predicting the 2025 NCAA Division I Women’s Basketball Tournament with a Multilevel Model

Efficiency models have had great success in predicting the outcomes of basketball games. The idea is simple: break everything down to possessions. Good teams score points on their possessions, while limiting opponents from scoring on their possessions. This basic principle underpins offensive and defensive ratings.

Just the raw numbers do not tell the whole story. The top scoring offense in 2025 was Murray State, the MVC champions ranked 185th in strength of schedule and whom the selection committee placed as an 11 seed; the top scoring defense in 2025 was 16 seed UNCG, ranked 244th in strength of schedule. It’s not just the totals: it’s also who you play against. A predictive model will need to be able to account for this.

Offensive and Defensive Rating Models

Everything goes back to possessions. For simplicity, I use a possession loss model, which Kubatko et al. (2007) define as¹

¹ Oliver (2004) and his work popularized a number of statistical approaches to analyzing basketball

\[ \begin{align} POSS_t &= FGA_t \\ &\quad + 0.475 \times FTA_t \\ &\quad - OREB_t \\ &\quad + TO_t \end{align} \]

where for team $t$

$FGA_t$ is field goal attempts
$FTA_t$ is free throw attempts
$OREB_t$ is offensive rebounds
$TO_t$ is turnovers

We can assume that each team gets roughly the same number of possessions per game.

I model the rating for each team as a combination of their offensive strength and their opponent’s defensive strength:

\[Eff_{i,j} = \beta_0 + \beta_{\text{home\_off}} \times \text{home} + \text{team}_{i} + \text{opponent}_{j} + \epsilon_{i,j}\]

where $\text{team}_{i}$ and $\text{opponent}_{j}$ are random effects for each team and opponent, respectively.

For the data, I will use the excellent {wehoop} package (Gilani and Hutchinson 2021).

Code

eff_form <- bf(
  efficiency | weights(weight) ~ 1 + home_off + (1|team_id) + (1|opponent_team_id),
  center = TRUE
)

prior <- c(
  prior(normal(1.0, 0.15), class = "Intercept"),
  prior(normal(0.1, 0.05), class = "b", coef = "home_off"),
  prior(cauchy(0, 2), class = "sd", group = "team_id"),
  prior(cauchy(0, 2), class = "sd", group = "opponent_team_id"),
  prior(cauchy(0, 1.5), class = "sigma")
)

bmodel <- brm(
  formula = eff_form,
  data = (team_game_data |> mutate(home_off = ifelse(home == 1, 1, 0))),
  chains = 5,
  iter = 4000,
  warmup = 2000,
  cores = 5,
  file =  here::here("notes/2025-wbb/data/eff_model2"),
  prior = prior
)

Results

The raw offense and defense scores can be thought of as answering the question: on a given possession, how many more points does this team score on offense and limit on defense against an average team?

Because this is a Bayesian model, the posterior represents thousands of probable ways the relative strengths of the teams can explain the observed outcomes (scores from the games).

Table 1: Small sample of draws from the posterior for two teams.

Figure 2: Histogram of draws from the posterior for two teams’ relative offensive ratings.

There are a few ways we could consider what team is the “best” from this model:

What is the team’s average (mean and median) rank across the posterior draws?
What percentage of games would we expect each team to win against an average team?

Table 2

Rank	Team	Mean Rank	Median Rank	Top Offense	Top Defense	Wins
1	UConn Huskies	1.3	1	76.61%	25.10%	99.83%
2	South Carolina Gamecocks	2.2	2	15.07%	21.52%	99.52%
3	Texas Longhorns	3.8	3	0.48%	22.28%	99.13%
4	Notre Dame Fighting Irish	5.2	5	0.28%	8.44%	98.70%
5	UCLA Bruins	5.6	5	1.08%	1.61%	98.72%
6	USC Trojans	7.3	7	0.10%	5.68%	98.02%
7	Duke Blue Devils	7.9	7	—	11.92%	98.07%
8	TCU Horned Frogs	9.1	8	5.67%	—	97.57%
9	West Virginia Mountaineers	11.9	11	—	2.47%	96.77%
10	Kansas State Wildcats	12.4	11	0.16%	0.01%	96.57%
11	Ole Miss Rebels	13.3	12	0.01%	0.12%	96.57%
12	LSU Tigers	14.1	13	0.07%	0.01%	96.00%
13	Baylor Bears	15.8	15	—	0.03%	95.87%
14	Tennessee Lady Volunteers	16.1	15	0.07%	—	95.86%
15	Oklahoma Sooners	17.6	16	0.01%	0.02%	94.95%
16	Alabama Crimson Tide	18.1	17	0.01%	0.01%	95.08%
17	NC State Wolfpack	19.2	18	0.01%	—	94.78%
18	Kentucky Wildcats	20.6	19	—	0.02%	94.51%
19	Ohio State Buckeyes	22.7	22	—	0.03%	93.78%
20	Iowa Hawkeyes	23.0	22	—	0.01%	93.78%
21	Vanderbilt Commodores	23.5	22	0.17%	—	93.76%
22	North Carolina Tar Heels	24.4	23	—	0.12%	93.44%
23	Michigan State Spartans	24.4	23	—	—	92.73%
24	Michigan Wolverines	27.1	26	0.01%	—	92.51%
25	Oklahoma State Cowgirls	27.8	27	—	—	91.88%

Simulating the Tournament

Seed	Team	R32	S16	E8	F4	Final	Champs
1	UCLA Bruins	99.45%	84.83%	57.80%	40.92%	15.43%	7.15%
16	Southern Jaguars	0.55%	0.06%	—	—	—	—
8	Richmond Spiders	52.90%	8.21%	3.28%	1.41%	0.31%	0.08%
9	Georgia Tech Yellow Jackets	47.10%	6.90%	2.55%	0.97%	0.14%	0.04%
5	Ole Miss Rebels	86.86%	43.46%	17.28%	9.92%	2.88%	0.88%
12	Ball State Cardinals	13.14%	1.99%	0.22%	0.04%	0.01%	0.01%
4	Baylor Bears	85.48%	51.09%	18.52%	10.08%	2.53%	0.81%
13	Grand Canyon Lopes	14.52%	3.46%	0.35%	0.14%	0.02%	—
6	Florida State Seminoles	56.53%	16.86%	7.52%	2.02%	0.32%	0.07%
11	George Mason Patriots	43.47%	11.31%	4.28%	1.23%	0.18%	0.04%
3	LSU Tigers	93.90%	70.37%	41.12%	16.97%	4.04%	1.26%
14	San Diego State Aztecs	6.10%	1.46%	0.24%	0.01%	—	—
7	Michigan State Spartans	54.90%	22.35%	10.52%	3.73%	0.59%	0.18%
10	Harvard Crimson	45.10%	16.85%	7.12%	2.17%	0.30%	0.06%
2	NC State Wolfpack	88.20%	58.06%	28.74%	10.36%	2.02%	0.55%
15	Vermont Catamounts	11.80%	2.74%	0.46%	0.03%	—	—

Seed	Team	R32	S16	E8	F4	Final	Champs
1	South Carolina Gamecocks	99.27%	92.07%	79.79%	60.09%	38.10%	21.25%
16	Tennessee Tech Golden Eagles	0.73%	0.12%	0.04%	—	—	—
8	Utah Utes	57.74%	5.21%	2.76%	1.01%	0.25%	0.04%
9	Indiana Hoosiers	42.26%	2.60%	1.14%	0.37%	0.10%	0.01%
5	Alabama Crimson Tide	79.21%	46.92%	9.99%	4.28%	1.41%	0.32%
12	Green Bay Phoenix	20.79%	6.54%	0.43%	0.07%	0.01%	—
4	Maryland Terrapins	80.35%	41.75%	5.53%	1.73%	0.35%	0.07%
13	Norfolk State Spartans	19.65%	4.79%	0.32%	0.07%	—	—
6	West Virginia Mountaineers	76.04%	44.63%	21.89%	7.22%	2.76%	0.78%
11	Columbia Lions	23.96%	7.85%	2.00%	0.32%	0.07%	—
3	North Carolina Tar Heels	91.65%	46.70%	16.15%	3.63%	0.98%	0.23%
14	Oregon State Beavers	8.35%	0.82%	0.05%	—	—	—
7	Vanderbilt Commodores	68.81%	17.04%	7.96%	1.87%	0.47%	0.12%
10	Oregon Ducks	31.19%	3.76%	1.03%	0.16%	0.01%	—
2	Duke Blue Devils	96.49%	78.49%	50.77%	19.17%	8.25%	2.79%
15	Lehigh Mountain Hawks	3.51%	0.71%	0.15%	0.01%	—	—

Seed	Team	R32	S16	E8	F4	Final	Champs
1	Texas Longhorns	99.91%	89.18%	69.38%	42.09%	22.32%	10.83%
16	William & Mary Tribe	0.09%	—	—	—	—	—
8	Illinois Fighting Illini	48.83%	5.26%	2.12%	0.58%	0.09%	0.03%
9	Creighton Bluejays	51.17%	5.56%	2.36%	0.57%	0.14%	0.04%
5	Tennessee Lady Volunteers	86.34%	46.12%	13.95%	5.33%	1.88%	0.51%
12	South Florida Bulls	13.66%	2.52%	0.17%	0.02%	—	—
4	Ohio State Buckeyes	79.23%	45.21%	11.19%	3.56%	1.07%	0.33%
13	Montana State Bobcats	20.77%	6.15%	0.83%	0.18%	—	—
6	Michigan Wolverines	57.04%	9.80%	3.61%	0.90%	0.30%	0.05%
11	Iowa State Cyclones	42.96%	5.82%	1.88%	0.51%	0.09%	0.01%
3	Notre Dame Fighting Irish	96.99%	83.73%	53.44%	28.61%	14.42%	6.41%
14	Stephen F. Austin Ladyjacks	3.01%	0.65%	0.11%	0.03%	—	—
7	Louisville Cardinals	51.88%	8.98%	1.91%	0.36%	0.05%	0.01%
10	Nebraska Cornhuskers	48.12%	7.96%	1.63%	0.34%	0.06%	0.01%
2	TCU Horned Frogs	98.61%	82.80%	37.42%	16.92%	6.82%	2.24%
15	Fairleigh Dickinson Knights	1.39%	0.26%	—	—	—	—

Seed	Team	R32	S16	E8	F4	Final	Champs
1	USC Trojans	97.80%	83.82%	54.94%	16.85%	9.74%	4.18%
16	UNC Greensboro Spartans	2.20%	0.36%	0.06%	—	—	—
8	California Golden Bears	45.61%	6.65%	2.20%	0.28%	0.07%	—
9	Mississippi State Bulldogs	54.39%	9.17%	3.48%	0.45%	0.11%	0.02%
5	Kansas State Wildcats	79.14%	42.89%	19.49%	4.74%	2.38%	0.86%
12	Fairfield Stags	20.86%	5.64%	1.16%	0.14%	0.06%	0.01%
4	Kentucky Wildcats	88.94%	49.62%	18.41%	3.42%	1.39%	0.39%
13	Liberty Flames	11.06%	1.85%	0.26%	0.01%	—	—
6	Iowa Hawkeyes	69.27%	28.95%	4.07%	1.51%	0.68%	0.20%
11	Murray State Racers	30.73%	7.52%	0.38%	0.12%	0.04%	0.01%
3	Oklahoma Sooners	83.02%	57.31%	8.57%	3.66%	1.71%	0.48%
14	Florida Gulf Coast Eagles	16.98%	6.22%	0.39%	0.08%	—	—
7	Oklahoma State Cowgirls	60.72%	3.16%	1.63%	0.60%	0.29%	0.10%
10	South Dakota State Jackrabbits	39.28%	1.26%	0.56%	0.13%	0.03%	0.01%
2	UConn Huskies	99.79%	95.52%	84.39%	68.01%	54.73%	36.53%
15	Arkansas State Red Wolves	0.21%	0.06%	0.01%	—	—	—

Putting the Model into Practice

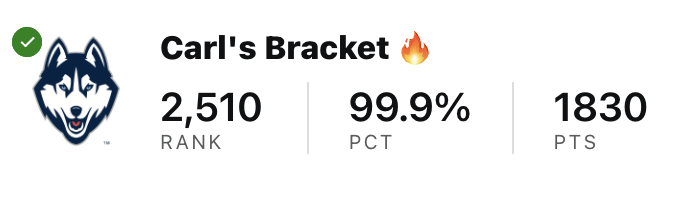
I used this model to help me create my bracket, ranking in the top 0.01% out of millions of submissions on ESPN. My bracket correctly predicted the national champion, the finals matchup, all four teams in the Final Four, 7/8 teams in the Elite Eight, and 15/16 teams in the Sweet Sixteen.

My final point total and rank on ESPN’s Tournament Challenge

References

Gilani, Saiem, and Geoffery Hutchinson. 2021. “Wehoop: Access Women’s Basketball Play by Play Data.” CRAN: Contributed Packages. The R Foundation. https://doi.org/10.32614/cran.package.wehoop.

Kubatko, Justin, Dean Oliver, Kevin Pelton, and Dan T Rosenbaum. 2007. “A Starting Point for Analyzing Basketball Statistics.” Journal of Quantitative Analysis in Sports 3 (3).

Oliver, Dean. 2004. Basketball on Paper: Rules and Tools for Performance Analysis. U of Nebraska Press.

--- title: Predicting the 2025 NCAA Division I Women's Basketball Tournament with a Multilevel Model description: Using offensive and defensive ratings to simulate the odds of cutting down the nets date: 2025-03-20 bibliography: bibliography.bib tags: [sports, brms] format: html: code-fold: true html-table-processing: none execute: warning: false error: false echo: false --- ```{r} #| label: setup library(tidyverse) library(brms) library(tidybayes) library(gt) library(furrr) # Tricks Positron to think we're RSTUDIO # Needed because of this issue: # https://github.com/posit-dev/positron/issues/5920 Sys.setenv(RSTUDIO = 1) game_weight <- function(days) { return(0.995 ^ days) } n_cores <- 6 my_gt_theme <- function(table) { return( table |> opt_table_font( font = c("Lato") ) |> tab_style( style = list( cell_text(weight = "bold") ), locations = cells_column_labels() ) ) } ``` Efficiency models have had great success in predicting the outcomes of basketball games. The idea is simple: break everything down to possessions. Good teams score points on their possessions, while limiting opponents from scoring on their possessions. This basic principle underpins offensive and defensive ratings. Just the raw numbers do not tell the whole story. The [top scoring offense](https://stats.ncaa.org/rankings/national_ranking?academic_year=2025.0&division=1.0&ranking_period=151.0&sport_code=WBB&stat_seq=111.0) in 2025 was Murray State, the MVC champions ranked [185th in strength of schedule](https://www.warrennolan.com/basketballw/2025/sos-rpi) and whom the selection committee placed as an 11 seed; the [top scoring defense](https://stats.ncaa.org/rankings/national_ranking?academic_year=2025.0&division=1.0&ranking_period=151.0&sport_code=WBB&stat_seq=112.0) in 2025 was 16 seed UNCG, ranked 244th in strength of schedule. It's not just the totals: it's also who you play against. A predictive model will need to be able to account for this. ## Offensive and Defensive Rating Models Everything goes back to possessions. For simplicity, I use a possession loss model, which @kubatko2007starting define as[^oliver] [^oliver]: @oliver2004basketball and his work popularized a number of statistical approaches to analyzing basketball $$ \begin{align} POSS_t &= FGA_t \\ &\quad + 0.475 \times FTA_t \\ &\quad - OREB_t \\ &\quad + TO_t \end{align} $$ where for team $t$ - $FGA_t$ is field goal attempts - $FTA_t$ is free throw attempts - $OREB_t$ is offensive rebounds - $TO_t$ is turnovers We can assume that each team gets roughly the same number of possessions per game. I model the rating for each team as a combination of their offensive strength and their opponent's defensive strength: $$Eff_{i,j} = \beta_0 + \beta_{\text{home\_off}} \times \text{home} + \text{team}_{i} + \text{opponent}_{j} + \epsilon_{i,j}$$ where $\text{team}_{i}$ and $\text{opponent}_{j}$ are random effects for each team and opponent, respectively. For the data, I will use the excellent [`{wehoop}`](https://wehoop.sportsdataverse.org/) package [@hutchinson_gilani_2021_wehoop]. ```{r} #| label: download-data #| cache: true # Only use data from before the tournament starts # (play-in games are fine) current_date <- as.Date("2025-03-20") seasons <- c(2025) teams <- wehoop::espn_wbb_teams() |> select(team_id, display_name, logo, color) schedule <- wehoop::load_wbb_schedule(seasons = seasons) %>% mutate(days_since = as.numeric(current_date - game_date)) %>% filter(game_date <= current_date) |> filter(home_id %in% teams$team_id & away_id %in% teams$team_id) team_boxes <- wehoop::load_wbb_team_box(seasons = seasons) |> filter(game_id %in% schedule$game_id) pbp <- wehoop::load_wbb_pbp(seasons = seasons) |> filter(game_id %in% schedule$game_id) game_periods <- pbp |> select(game_id, period_number) |> arrange(desc(period_number)) |> distinct(game_id, .keep_all = TRUE) |> # Account for overtime games mutate(minutes = 40 + (period_number - 4) * 5) team_game_data <- inner_join( (team_boxes |> select(game_id, season, team_id, team_home_away, team_score, opponent_team_id, opponent_team_score, field_goals_attempted, offensive_rebounds, turnovers, free_throws_attempted)), (schedule %>% select(id, neutral_site, conference_competition, days_since)), by = c("game_id" = "id") ) %>% inner_join( game_periods, by = "game_id" ) |> mutate(possessions = field_goals_attempted - offensive_rebounds + turnovers + (0.475 * free_throws_attempted)) |> mutate(efficiency = team_score / possessions) %>% mutate(weight = game_weight(days_since)) %>% mutate(home = ifelse(neutral_site == 1, 0, ifelse(team_home_away == "home", 1, 0))) possessions <- team_game_data |> select(team_id, game_id, possessions) |> # Get total possessions for each game_id group_by(game_id) |> summarize(possessions = sum(possessions)) ``` ```{r} #| label: model-possessions #| eval: false possession_data <- left_join( (team_game_data |> select(game_id, team_id, weight, minutes)), (possessions |> select(game_id, possessions)), by = "game_id" ) |> mutate(pace = possessions / minutes) possession_prior <- c( prior(normal(0, 5), class = "Intercept"), prior(cauchy(0, 2), class = "sd", group = "team_id") ) possession_model <- brm( formula = bf( pace | weights(weight) ~ 1 + (1 | team_id), center = TRUE ), data = possession_data, chains = 4, iter = 2000, warmup = 1000, cores = 4, file = here::here("notes/2025-wbb/data/possession_model"), # thin = 1, prior = possession_prior ) ``` ```{r} #| label: model-efficiency #| echo: true eff_form <- bf( efficiency | weights(weight) ~ 1 + home_off + (1|team_id) + (1|opponent_team_id), center = TRUE ) prior <- c( prior(normal(1.0, 0.15), class = "Intercept"), prior(normal(0.1, 0.05), class = "b", coef = "home_off"), prior(cauchy(0, 2), class = "sd", group = "team_id"), prior(cauchy(0, 2), class = "sd", group = "opponent_team_id"), prior(cauchy(0, 1.5), class = "sigma") ) bmodel <- brm( formula = eff_form, data = (team_game_data |> mutate(home_off = ifelse(home == 1, 1, 0))), chains = 5, iter = 4000, warmup = 2000, cores = 5, file = here::here("notes/2025-wbb/data/eff_model2"), prior = prior ) ``` ## Results ```{r} #| label: fig-ratings #| fig-cap: Offensive and defensive ratings for top teams in the NCAA women's basketball tournament. Teams near the top right of the graph have the best overall ratings. library(ggpath) offense <- bmodel %>% spread_draws(r_team_id[team_id, ]) %>% group_by(team_id) %>% summarize( mean = mean(r_team_id), lower = quantile(r_team_id, 0.025), upper = quantile(r_team_id, 0.975) ) %>% arrange(desc(mean)) defense <- bmodel %>% spread_draws(r_opponent_team_id[opponent_team_id, ]) %>% group_by(opponent_team_id) %>% summarize( mean = mean(r_opponent_team_id), lower = quantile(r_opponent_team_id, 0.025), upper = quantile(r_opponent_team_id, 0.975) ) %>% arrange(mean) team_draws <- inner_join( (offense |> select(team_id, mean) |> rename(offense = mean)), (defense |> select(opponent_team_id, mean) |> rename(defense = mean, team_id = opponent_team_id)), by = "team_id" ) |> left_join(teams, by="team_id") team_draws %>% mutate(s = offense - defense) |> arrange(desc(s)) |> head(25) |> ggplot(aes(x = offense, y = defense)) + geom_from_path(aes(path = logo), width = 0.05) + labs( title = "Top Teams by Scoring Efficiency", subtitle = "2025 Season", x = "Offensive Efficiency", y = "Defensive Efficiency" ) + coord_fixed() + scale_y_reverse() + theme_minimal() ``` The raw offense and defense scores can be thought of as answering the question: on a given possession, how many more points does this team score on offense and limit on defense against an average team? ```{r} posterior_samples <- as_draws_df(bmodel) team_id_effects <- posterior_samples[, grep("^r_team_id", names(posterior_samples)), drop = FALSE] team_id_long <- team_id_effects %>% mutate(.draw = 1:n(), .chain = rep(1:5, each = 2000)) %>% pivot_longer( cols = starts_with("r_team_id"), names_to = "team_id", values_to = "team_effect" ) %>% mutate(team_id = gsub("r_team_id\\[(.+),Intercept\\]", "\\1", team_id)) # Get the random effects for opponent_team_id opponent_effects <- posterior_samples[, grep("^r_opponent_team_id", names(posterior_samples)), drop = FALSE] # Reshape to long format opponent_long <- opponent_effects %>% mutate(.draw = 1:n(), .chain = rep(1:5, each = 2000)) %>% pivot_longer( cols = starts_with("r_opponent_team_id"), names_to = "opponent_team_id", values_to = "opponent_effect" ) %>% mutate(opponent_team_id = gsub("r_opponent_team_id\\[(.+),Intercept\\]", "\\1", opponent_team_id)) ``` Because this is a Bayesian model, the posterior represents thousands of probable ways the relative strengths of the teams can explain the observed outcomes (scores from the games). ```{r} #| label: tbl-offense-draws #| tbl-cap: Small sample of draws from the posterior for two teams. #| column: margin #| eval: false team_id_long |> filter(team_id == 41 | team_id == 2579) |> mutate(team_id = as.integer(team_id)) |> filter(.draw <= 3) |> select(.draw, team_id, team_effect) |> left_join(teams, by = "team_id") |> select(.draw, display_name, team_effect) |> gt::gt() |> cols_label( .draw = "Draw", display_name = "Team", team_effect = "Offense" ) |> my_gt_theme() ``` ```{r} #| label: fig-relative-offense #| fig-cap: Histogram of draws from the posterior for two teams' relative offensive ratings. #| fig-cap-location: top #| cap-location: top #| fig-width: 4 #| fig-height: 3.5 team_id_long |> mutate(team_id = as.integer(team_id)) |> filter(team_id == 41 | team_id == 2579) |> left_join(teams, by = "team_id") |> rename(Team = display_name) |> ggplot(aes(x = team_effect, fill = Team, y = after_stat(count / sum(count)))) + geom_histogram(alpha = 1, position = "dodge", binwidth=0.01) + labs( x = "Relative Offensive Rating", y = "Proportion" ) + theme_minimal() + theme(legend.position='bottom') ``` There are a few ways we could consider what team is the "best" from this model: - What is the team's average (mean and median) rank across the posterior draws? - What percentage of games would we expect each team to win against an average team? ```{r} #| label: tbl-rankings #| tbl-caption: Top teams in the country for the 2024--2025 season based on their expected number of wins against an average team. top_offense <- team_id_long |> group_by(.draw, .chain) |> slice_max(order_by = team_effect, n = 1) |> ungroup() |> count(team_id) |> arrange(desc(n)) |> mutate(team_id = as.integer(team_id)) |> mutate(n = n/sum(n)) top_defense <- opponent_long |> group_by(.draw, .chain) |> slice_min(order_by = opponent_effect, n = 1) |> ungroup() |> count(opponent_team_id) |> rename(team_id = opponent_team_id) |> arrange(desc(n)) |> mutate(team_id = as.integer(team_id)) |> mutate(n = n/sum(n)) intercepts <- posterior_samples |> select(b_Intercept, b_home_off, sigma, sd_opponent_team_id__Intercept, sd_team_id__Intercept) |> mutate(.draw = 1:n(), .chain = rep(1:5, each = 2000)) simulations <- inner_join( team_id_long, (opponent_long |> rename(team_id = opponent_team_id)), by = c(".draw", ".chain", "team_id") ) |> rename(offense = team_effect, defense = opponent_effect) |> inner_join(intercepts, by = c(".draw", ".chain")) |> mutate( score = (b_Intercept + offense + rnorm(n(), 0, sigma)), opp_score = (b_Intercept + defense + rnorm(n(), 0, sigma)), ) |> mutate(win = score > opp_score) team_ranks <- simulations |> mutate(s = offense - defense) |> group_by(.draw) |> mutate(r = rank(-s)) |> ungroup() |> group_by(team_id) |> summarize( mean_rank = mean(r), median_rank = median(r) ) |> arrange(mean_rank) |> mutate(team_id = as.integer(team_id)) simulations |> filter(win) |> #group_by(team_id) |> count(team_id) |> mutate(wins = n/max(simulations$.draw)) |> mutate(team_id = as.integer(team_id)) |> left_join(team_ranks, by = "team_id") |> arrange(mean_rank) |> inner_join(teams, by = "team_id") |> mutate(rank = 1:n()) |> left_join( full_join( (top_offense |> rename(top_offense = n)), (top_defense |> rename(top_defense = n)), by = "team_id" ), by = "team_id" ) |> head(25) |> mutate(c = " ") |> select(c, color, rank, display_name, mean_rank, median_rank, top_offense, top_defense, wins) |> mutate(color = paste("#", color, sep="")) |> gt::gt() |> tab_style( style = list(cell_fill(color = from_column(column = "color"))), locations = cells_body(columns = c) ) |> fmt_percent( columns = c(wins, top_offense, top_defense) ) |> fmt_number( columns = c(mean_rank), decimals = 1 ) |> cols_hide(columns = c(color)) |> sub_missing( columns = c(top_offense, top_defense), missing_text = "---" ) |> cols_label(c = "", rank = "Rank", display_name = "Team", wins = "Wins", top_offense = "Top Offense", top_defense = "Top Defense", mean_rank = "Mean Rank", median_rank = "Median Rank") |> my_gt_theme() ``` ## Simulating the Tournament ```{r} # get seeds tourney_games <- wehoop::load_wbb_schedule(seasons = seasons) |> filter(str_starts(notes_headline, "NCAA Women's Championship")) |> filter(str_ends(notes_headline, "1st Round")) ``` ```{r} #| label: get-games-df sorted_games <- tourney_games |> mutate(regional_number = str_extract(notes_headline, "(?<=Regional )\\d+")) |> arrange(regional_number) |> select(game_id, regional_number, home_id, away_id, home_current_rank, away_current_rank) |> # Create opponent_id columns before pivoting mutate( home_opponent_id = away_id, away_opponent_id = home_id ) |> pivot_longer( cols = c(home_id, away_id), names_to = "team_type", values_to = "team_id" ) |> # Also pivot opponent IDs mutate( opponent_id = if_else(team_type == "home_id", home_opponent_id, away_opponent_id), seed = if_else(team_type == "home_id", home_current_rank, away_current_rank), is_home = team_type == "home_id" ) |> select(game_id, regional_number, team_id, opponent_id, seed, is_home) |> group_by(game_id) %>% # Create a matchup order value based on the lower seed in each game mutate( min_seed = min(seed), # Create bracket ordering (1,16,8,9,5,12,4,13,6,11,3,14,7,10,2,15) bracket_order = case_when( min_seed == 1 ~ 1, min_seed == 8 ~ 2, min_seed == 5 ~ 3, min_seed == 4 ~ 4, min_seed == 6 ~ 5, min_seed == 3 ~ 6, min_seed == 7 ~ 7, min_seed == 2 ~ 8, TRUE ~ 9 # Fallback for any unexpected seeds ) ) %>% ungroup() %>% mutate( regional_order = case_when( regional_number == "1" ~ 1, regional_number == "4" ~ 2, regional_number == "2" ~ 3, regional_number == "3" ~ 4, TRUE ~ 5 )) |> # Sort by regional number first, then bracket order, then seed arrange(regional_order, bracket_order, seed) %>% # Remove the working columns we added select(-min_seed, -bracket_order, -regional_order) n_sims <- 1 tourney_sims <- inner_join( team_id_long, (opponent_long |> rename(team_id = opponent_team_id)), by = c(".draw", ".chain", "team_id") ) |> rename(offense = team_effect, defense = opponent_effect) |> inner_join(intercepts, by = c(".draw", ".chain")) |> mutate(team_id = as.integer(team_id)) |> filter(team_id %in% sorted_games$team_id) |> uncount(n_sims) |> # This will expand each row by n_sims group_by(team_id) |> mutate(sim_id = row_number()) |> ungroup() ``` ```{r} #| label: simulation-functions simulate_round <- function(df) { if ("win" %in% names(df)) { df <- df |> select(game_id, team_id, opponent_id, seed, is_home, sim_id, win) df <- df |> filter(win) |> mutate(game_id = as.integer(gl(n = n()/2, k = 2, labels = seq_len(n() / 2)))) |> group_by(game_id) %>% mutate( # Store all team_ids for this game in a list all_teams = list(team_id), # For each row, find the opponent team_id opponent_id_new = map_dbl(row_number(), function(i) { current_team <- team_id[i] other_teams <- setdiff(unlist(all_teams), current_team) if(length(other_teams) == 1) return(other_teams) else return(NA_real_) }) ) %>% ungroup() %>% # Replace the old opponent_id with the new one select(-opponent_id, -all_teams) %>% rename(opponent_id = opponent_id_new) } else { df <- df |> select(game_id, team_id, opponent_id, seed, is_home, sim_id) } rnd = 7 - log2(nrow(df)) df <- df |> mutate(home_adv = (is_home & rnd <= 2 & seed <= 4)) df <- left_join( df, (tourney_sims |> select(sim_id, team_id, offense, b_Intercept, b_home_off, sigma, sd_opponent_team_id__Intercept, sd_team_id__Intercept)), by = c("sim_id", "team_id") ) |> left_join( (tourney_sims |> select(sim_id, team_id, defense) |> rename(opponent_id = team_id)), by = c("sim_id", "opponent_id") ) rnd <- df |> mutate(score = (b_Intercept + b_home_off*home_adv + offense + defense + rnorm(n(), 0, sigma))) |> group_by(game_id) |> # Group by game_id to compare scores within each game mutate( win = score == max(score) # TRUE if the team has the highest score in the game ) |> ungroup() return(rnd |> select(game_id, team_id, opponent_id, seed, is_home, sim_id, win, score)) } run_round_sim <- function(df) { return( df |> group_by(sim_id) |> group_map(~simulate_round(.x), .keep=TRUE) |> bind_rows() ) } run_round <- function(df) { df %>% mutate(sim_group = sim_id %% n_cores^2) |> group_by(sim_group) |> group_split() |> future_map_dfr(run_round_sim, .progress = TRUE, .options = furrr_options(seed = TRUE) ) # Run in parallel # .options = furrr_options(seed = 472839710) } ``` ```{r} #| label: run-simulations #| cache: true # Run in parallel plan(multisession, workers = n_cores) my_df <- left_join( sorted_games, (tourney_sims |> select(team_id, sim_id)), by = "team_id" ) r1 <- my_df %>% run_round() |> mutate(rnd = 1) r2 <- run_round(r1) |> mutate(rnd = 2) r3 <- run_round(r2) |> mutate(rnd = 3) r4 <- run_round(r3) |> mutate(rnd = 4) r5 <- run_round(r4) |> mutate(rnd = 5) r6 <- run_round(r5) |> mutate(rnd = 6) results <- rbind(r1, r2, r3, r4, r5, r6) ``` ```{r} team_odds <- results |> filter(win) |> group_by(rnd, team_id) %>% summarise(count = n()/max(my_df$sim_id), .groups = "drop") %>% filter(rnd >= 1, rnd <= 6) %>% pivot_wider(names_from = rnd, values_from = count, names_prefix = "round_") |> arrange(desc(round_4)) |> left_join(teams, by = "team_id") |> mutate(c = " ") |> select(c, color, team_id, display_name, round_1, round_2, round_3, round_4, round_5, round_6) |> mutate(color = paste("#", color, sep="")) |> left_join((sorted_games |> select(team_id, regional_number, seed)), by = "team_id") format_regional_table <- function(df) { table <- df |> mutate( # Create bracket ordering (1,16,8,9,5,12,4,13,6,11,3,14,7,10,2,15) bracket_order = case_when( seed == 1 ~ 1, seed == 16 ~ 2, seed == 8 ~ 3, seed == 9 ~ 4, seed == 5 ~ 5, seed == 12 ~ 6, seed == 4 ~ 7, seed == 13 ~ 8, seed == 6 ~ 9, seed == 11 ~ 10, seed == 3 ~ 11, seed == 14 ~ 12, seed == 7 ~ 13, seed == 10 ~ 14, seed == 2 ~ 15, seed == 15 ~ 16, TRUE ~ 17 # Fallback for any unexpected seeds ) ) |> arrange(bracket_order) |> select(c, seed, display_name, round_1, round_2, round_3, round_4, round_5, round_6, color) |> gt::gt() |> fmt_percent( columns = c(round_1, round_2, round_3, round_4, round_5, round_6) ) |> tab_style( style = list(cell_fill(color = from_column(column = "color"))), locations = cells_body(columns = c) ) |> cols_hide(columns = c(color)) |> sub_missing( columns = c(round_2, round_3, round_4, round_5, round_6), missing_text = "---" ) |> cols_label( c = "", seed = "Seed", display_name = "Team", round_1 = "R32", round_2 = "S16", round_3 = "E8", round_4 = "F4", round_5 = "Final", round_6 = "Champs" ) |> my_gt_theme() return(table) } ``` ::: {.panel-tabset .column-page-right} ### Regional 1 ```{r} team_odds |> filter(regional_number == "1") |> format_regional_table() ``` ### Regional 2 ```{r} team_odds |> filter(regional_number == "2") |> format_regional_table() ``` ### Regional 3 ```{r} team_odds |> filter(regional_number == "3") |> format_regional_table() ``` ### Regional 4 ```{r} team_odds |> filter(regional_number == "4") |> format_regional_table() ``` ::: ## Putting the Model into Practice I used this model to help me create my bracket, ranking in the top 0.01% out of millions of submissions on ESPN. My bracket correctly predicted the national champion, the finals matchup, all four teams in the Final Four, 7/8 teams in the Elite Eight, and 15/16 teams in the Sweet Sixteen. The big things I got wrong: TCU over Notre Dame and Kansas State over Kentucky. ![My final point total and rank on ESPN's Tournament Challenge](./images/bracket_results.png)